IEEE Signal Processing Society 1999 Workshop on Multimedia Signal Processing
September 13-15, Copenhagen, Denmark
Electronic Proceedings
© 1999 IEEE
PROGRESSIVE BROWSING OF 3D MODELS
Abstract
High-speed desktop computers, capable of rendering complex 3-D models, are becoming more commonplace, resulting in increasing interest in virtual reality systems. Virtual Reality Modelling Language (VRML) has become the de-facto standard for the description of virtual worlds over the Internet, yet the current version (VRML97) lacks capabilities for progressive transfer. This paper describes the implementation of a browser that allows the progressive transfer and simultaneous viewing of 3-D models, stored in a progressive format on a web server, using a codec based on MPEG-4 verification model source code. The authors then implement their own codec that is progressive per-vertex rather than per-level. This approach also has the benefit that it does not alter the vertex coordinates. Finally, a watermarking scheme, based on the second codec, is proposed.
Table of Contents
- Introduction
- Progressive browser using MPEG-4 codec
- Progressive browser using vertex decimation codec
- Comparison between the two methods
- Watermarking
- Conclusion
- References
Introduction
With the advent of high-speed desktop computers capable of rendering complex 3-D models, there has been increasing interest in virtual reality systems. In such systems the user is immersed in an interactive 3-D environment, where the user can "walk" around and explore the different parts of the virtual world. Virtual Reality Modelling Language (VRML) has become the de-facto standard for the description of such virtual worlds on the Internet. Although the advantage of this format is that it is a straightforward and open format, VRML files are often large and take a long time to download. In addition, the current standard requires the entire file to be downloaded before even a small part of the world may be viewed.
Much work has been done to overcome these problems, such as a compressed binary format (a list of current Web3D working groups can be found at [1]). The MPEG-4 Synthetic/Natural Hybrid Coding subgroup (MPEG-4 SNHC) is also working in similar areas [2].
<-- Back to Table of Contents>
Progressive browser using MPEG-4 codec
We implemented a browser that downloads 3D models in a progressive format, based on the MPEG-4 verification model source code [3]. The system consists of two parts: an encoder, which encodes a VRML 2.0 file with one IndexedFaceSet (with no properties) into our .pvl (Progressive VrmL) format, and a browser that can view these .pvl files from a local file or a web site specified by a URL. The coding of 3D models is based on an early (Oct ’98) version of source code for a verification model for MPEG-4, using the algorithm Progressive Forest Split [4].
In the bitstream, the model is coded in layers of increasing complexity, each new layer building upon the previous layers. The browser can then render the best approximation to the model as the file is being downloaded, allowing the user to examine the coarse versions of the model and to stop the download at any time. We have set up the browser so that it is launched automatically from Internet Explorer. The browser demonstrates the feasibility and usefulness of progressive encoding for 3D models for transfer over the Internet.
Progressive VRML encoder

The encoder consists of two programs: pfsSimplify and pfc (see Fig. 1). pfsSimplify does the work of deciding which vertices lie on which layers, storing this information into the .cls file. pfc then takes this .cls file and applies binary coding to compress the file into the .pvl format. It takes the connectivity information and stores it using arithmetic coding, while the vertex locations and displacements are stored as raw floating-point.
Progressive VRML browser
The browser is used to view .pvl files locally or from the web (see Fig. 2). The .pvl file is placed onto a web server, and the browser connects to it and requests the file, using HyperText Transfer Protocol (HTTP). Once sufficient bits are downloaded from the server to display the next level of detail, the new model is updated on the screen. While the file is being downloaded the user can change his viewpoint to study the model and if the user is unsatisfied with the model he may stop downloading at any time. Fig. 3 shows levels 0, 3, 6 and 9 of the file opt-horse.pvl, coded in 10 levels, as it is being downloaded.




Fig. 3. Levels 0, 3, 6 and 9
<-- Back to Table of Contents>
Progressive browser using vertex decimation codec
The method of progressive encoding described above has some disadvantages. Firstly, each level of detail must be loaded in its entirety before the model is updated. This is especially a problem for the last level, which usually takes up a large portion of the entire file. Should the downloading be interrupted halfway through a level, the algorithm cannot produce a partial layer based on the bits sent up to that point. Secondly, the vertex coordinates in all the levels except the final level need not correspond to actual vertices in the original model, which makes it difficult to handle the mapping of vertex properties such as texture coordinates.
We now describe our own algorithm to address these issues. To encode a 3D model, we simplify it by successively removing vertices in a process called vertex decimation, until we are left with a base mesh which has a fraction of the vertices and triangles in the original model. To send a 3D model, the algorithm starts by sending the base mesh, which is simply the vertex positions and triangle vertices as in an IndexedFaceSet in VRML. From this base mesh enhancements to the model are sent, vertex by vertex, until all the vertices are restored. The process of vertex decimation is as follows: assuming the mesh is triangular, there is a ring of triangles that surround every vertex. Vertices which have extraneous triangles connected to them, and vertices which have surrounding triangles that do not form a closed ring, are not decimated by this algorithm, so as not to destroy the topology of the model. After we remove the vertex, we will have to reconnect the mesh to fill up the hole left by the decimation, while keeping the mesh triangular. The method used is simply to start at an edge in the hole left behind by the decimation, and to proceed in a zigzag fashion to re-triangulate the hole. For example, in Fig. 4, the vertex surrounded by 6 triangles is removed and re-triangulated with 4 triangles, thus removing one vertex and 2 triangles.
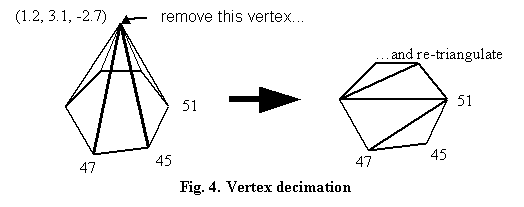
Each decimation can be encoded as a seven-tuple: the two indices of the vertices on the edge on which we start the re-triangulation, the index of the vertex from which to start the zigzag triangulation, the number of triangles to traverse, and the x, y, z coordinates of the new vertex. Vertices are numbered in the order they are sent in the base mesh, and each new vertex is assigned the next available index. The decimation in Fig. 4 would be encoded as (47, 45, 51, 4, 1.2, 3.1, -2.7). To ensure that vertices are sent in the order of perceptual importance, we must have a way of measuring the importance of each vertex. One method is to use the distance between the vertex and the mean of the vertices on the base. The measure we implemented is to estimate the difference in the volume caused by the decimation, by forming tetrahedrons with the removed vertex as the apex and the new triangles as the base, and adding up the volumes of these tetrahedrons.
Our algorithm is similar to [5], but simpler. No predictive coding is used for coordinates, our re-triangulation is always in a zigzag fashion, and we used the volume of tetrahedrons instead of distance to mean of base for the perceptual measure.
<-- Back to Table of Contents>
Comparison between the two methods
Both codecs were applied to eight VRML models obtained from public sources. As can be seen from Table 1, there was a saving of about 50% for the file size for Method 1 (MPEG-4 codec), and 59% for Method 2 (our codec), despite the fact that the files were progressively encoded. Much of the savings comes from binary encoding as VRML files contain whitespace and numbers are plain ASCII. We can also see that Method 2 uses fewer bits than Method 1 to encode the same file (although there are enhancements for Method 1, such as coding vertex coordinates using linear prediction, which we did not implement). The codec for Method 2 is also of lower complexity, does not move the vertex coordinates, and has better granularity. The browser constantly updates the model as the bits are received, rather than only being able to update at each level.
What is more important is the downloading time for the models, especially the time taken to view the first level of detail (see Table 2). The first level of detail for all the models for both methods were rendered in less than 2 seconds, giving the user a very good idea of what the complete model would look like. A copy of the browser and progressive files for both methods can be obtained from http://amp.ece.cmu.edu
filename |
no. of triangles |
no. of vertices |
original size (bytes) |
encoded size (bytes) method 1 |
encoded size (bytes) method 2 |
| opt-eight.wrl | 1536 |
766 |
51994 |
23286 |
21756 |
| opt-shape.wrl | 5120 |
2562 |
166971 |
83705 |
72524 |
| beethoven.wrl | 5030 |
2655 |
181545 |
108328 |
76040 |
| triceratops.wrl | 5660 |
2832 |
193399 |
94360 |
80092 |
| opt-pieta.wrl | 6976 |
3476 |
236819 |
136322 |
98868 |
| opt-femur.wrl | 7798 |
3897 |
269421 |
147434 |
110528 |
| opt-skull.wrl | 22104 |
10952 |
774743 |
392298 |
313084 |
| opt-horse.wrl | 22258 |
11135 |
792104 |
346691 |
315432 |
Table 1. Comparison of filesizes between original files and encoded files
filename |
original |
method 1 |
method 2 |
to load first level (both methods) |
| opt-eight.wrl | 18 |
8 |
8 |
<1 |
| opt-shape.wrl | 58 |
29 |
25 |
<1 |
| beethoven.wrl | 63 |
38 |
26 |
1 |
| triceratops.wrl | 67 |
33 |
28 |
1 |
| opt-pieta.wrl | 82 |
47 |
34 |
1 |
| opt-femur.wrl | 94 |
51 |
38 |
1 |
| opt-skull.wrl | 269 |
136 |
109 |
2 |
| opt-horse.wrl | 275 |
120 |
110 |
2 |
Table 2. Download times for original files and encoded files on a 28.8k modem in seconds
<-- Back to Table of Contents>
Watermarking
The per-vertex method of progressive encoding provides us with a useful product: it gives the vertices in the model an ordering. This ordering is resilient to the translation, rotation and scaling of the model. With such an ordering, it is possible to embed a pseudo-random sequence into a characteristic of each vertex, such as the distance between the vertex and the mean of the base.
Let t be the sequence of values of the distance between the vertex and the mean of the base, in the encoding order, and let w be a pseudo-random sequence we generate. Assume that t and w are independent, and that they are zero mean. If we take t, a sample from the "signal", and w, a sample from the "watermark", and multiply them together,
E (wt) = 0 Var (wt) = E (w2t2) – E2 (wt) = Var (w) Var (t)
If, on the other hand, we add w to t (embedding the watermark), and then multiply with w, we get
E (w(t+w)) = E (wt) + E (w2) = Var (w) Var (w(t+w)) » Var (w) Var (t)
The difference in the expected values gives us a way to detect if the watermark exists. We use this in our watermarking algorithm.
To embed the watermark:
- Determine the variance of the signal t
- Calculate the variance of w required to give us the required confidence level, based on Var (t) as well as n, the length of the sequence.
- Generate w the same length as t, using a seed value for the pseudorandom sequence
- Store s = w + t as the watermarked signal.
To detect if the watermark exists:
- Calculate the variance of s
- Estimate the variance of w, assuming Var (s) = Var (w) + Var (t)
- Regenerate w using the same seed value
- Calculate z = S ( ws ) (i.e. multiply each value of s with the corresponding value of w and sum it up)
- By central limit theorem,
if s is not watermarked, z ~ N(0, n Var (w) Var (t))
if s is watermarked, z ~ N(n Var(w), n Var(w) Var(t)) - Declare s watermarked if z > n Var(w) / 2
A look at the distribution of distances to mean of base shows us that the sequence is not zero mean and has an exponentially decreasing trend (Fig. 5, top right). To work around this problem, the sequence is broken up into blocks (we used 100 vertices per block), and the mean is subtracted from each block to produce a sequence that is zero-mean. The amplitude of the watermark is adjusted for each block (Fig. 5, bottom left), and this helps make the watermark less visible as points on flat surfaces are jittered less. To detect a watermark, we calculate z for each block, and normalize by dividing by n Var (w) / 2. If the average of these normalized z values is greater than 1, then the watermark is detected.
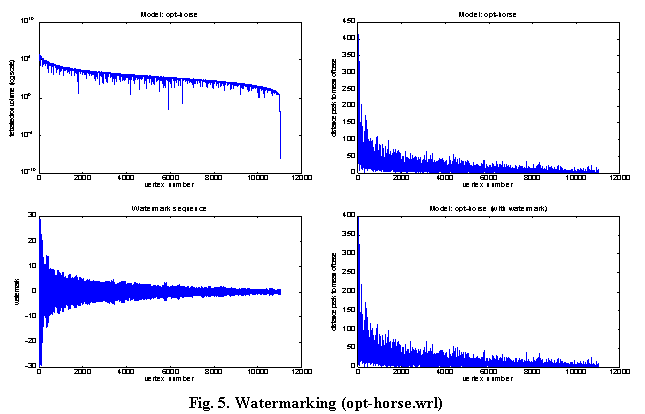


Fig. 6. Two cows. The cow on the right is watermarked.
The graphs in Fig. 5 are applied to the model opt-horse.wrl, which has 11135 vertices. The model in Fig. 6 is cow.wrl and it has 3066 vertices and 5804 triangles. The confidence level used for each block is 90%, and the overall confidence level is greater than 90% as we use the average value of z over several blocks in determining whether the model is watermarked. (Note that this scheme may be called "progressive watermarking", as the confidence of the watermark increases as more and more vertices are sent. It is straightforward to apply this concept to progressively coded audio, image and video as well.)
We watermarked our 8 models at 90% per block, then ran the watermarked and non-watermarked versions through the detector. The watermarks in all the watermarked models were detected, with an average value of 2.29. No watermark in any of the non-watermarked models was detected, with an average value of 0.29. We watermarked opt-horse.wrl with pseudo-random seed 0, and tested it with 1000 seeds (0 to 999). Only seed 0 was detected as the watermark, while the maximum value in the remaining 999 seeds was 0.42, well below the value 1.0 that would trigger a false alarm.
The results show that this watermarking scheme is reliable while not affecting the perceptual quality of the models too much (see Fig. 6), and that a large number of different watermarks are possible by varying the pseudo-random seed. However, these results assume that the ordering of the vertices is preserved. If the watermarked model is saved back into a non-progressive VRML file and re-encoded, the ordering of the vertices would not be the same, as the vertex coordinates were moved by the watermark, and as this ordering is required for the pseudo-random sequence, the watermark would be lost. There are some solutions to this: (a) the watermarked model can be re-coded, and the mapping between the vertex orderings can be saved and used to detect the watermark (b) the watermark can be placed on a characteristic that is independent of ordering, such as vertex colour (c) the user may be forbidden to change the ordering of the vertices, by restricting the client program in a web streaming environment, or (d) the original model may be used to match vertices and restore the ordering.
<-- Back to Table of Contents>
Conclusion
In this paper we demonstrated the feasibility of progressively coded 3D models. We created tools that coded VRML files into progressive bitstreams, and browsers that allow the user to view such progressive files as they are downloaded from the web. We also proposed a scheme for watermarking such files. For future extension of this work, we believe the progressive encoding scheme can be extended to create an interactive client-server system, where the server serves additional vertex information based on the viewpoint of the client, so that bandwidth is not wasted on sending vertices that are not currently visible to the client. We also feel that the watermarking scheme can be made more robust and reliable. An open problem we encountered in creating our watermarking scheme is finding a reliable way to order points in a mesh, which we will further investigate.
<-- Back to Table of Contents>
References
[1] Web3D Consortium Working Groups, http://www.web3d.org/fs_workinggroups.htm
[2] MPEG-4 SNHC web page,
http://www.es.com/mpeg4-snhc[3] MPEG-4 SNHC, Gabriel Taubin, editor, "SNHC Verification Model 9.0 [3D Mesh Encoding]", W2301, 7/10/98
[4] G. Taubin and J. Rossignac, "Geometric Compression through Topological Surgery", ACM Transactions on Graphics, 1998. Also IBM Research TR RC-20340, Jan 1996.
[5] J. Li and J. Kuo, "Progressive Coding of 3-D Graphics Models", Proceedings of the IEEE, Vol. 86, No. 6, June 1998
[6] R. Ohbuchi, H. Masuda and M. Aono, "Watermarking Three-Dimensional Polygonal Models Through Geometric and Topological Modifications", IEEE Journal on Selected Areas in Communications, Vol. 16, No. 4, May 1998