 |
About AMP Lab Projects Downloads Publications People Links
Project - Sampling Analysis for Image-Based Rendering
Image-based rendering (IBR) has attracted many attentions recently. When enough images are captured, IBR requires little or no geometry of the scene, which is idea for real scenes. The rendering algorithm of IBR is independent of the scene complexity, which is also very attractive. IBR can often provide very realistic rendering results that those rendered with traditional methods.
We are particularly interested in interpolation-based image-based rendering. As often no geometry is available for real scenes, IBR need to capture many images. The sampling problem of IBR is thus very important. In this project, we want to study the IBR sampling problem from with classic methods in signal processing.
The spectral analysis with surface plenoptic function
We define surface plenoptic function as a function on the object surface that describes light rays emitted/reflected from the surface. The full surface plenoptic function is 6D: time (1D), wavelength (1D), point on the surface S (2D), and azimuth and elevation angles (2D) the light ray is emitted. Under the free space assumption (light rays don't change their radiance if not blocked), surface plenoptic is equivalent to the full plenoptic function proposed by Adelson and Bergen.
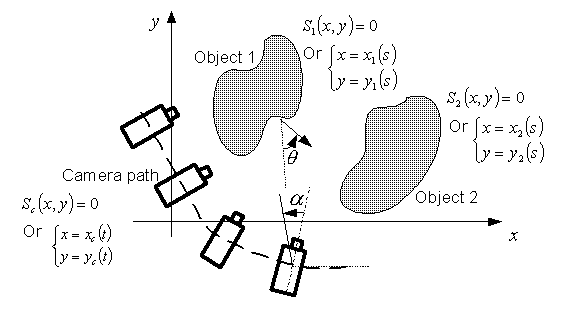
We give a 2D world example in the above figure. The object surface can be parameterized with one variable, e.g., the arc length. With also the emission direction theta , the surface plenoptic function is 2D.
A general IBR representation captures images of the scene along a path. This is also shown above. IBR representation is described by the arc length on the camera path and also the receiving angle of light rays. We need to know what is the minimum sampling rate for the IBR representation.
We notice that there is a mapping between the SPF and the IBR representation due to the light ray correspondence. Our strategy is to find the mapping between them. By assuming some spectral property of the SPF, we can derive the spectrum of the IBR representation. For detailed information, please refer to our technical report.
Generalized plenoptic sampling
We view the IBR sampling problem as a high-dimensional sampling problem. We then apply the sampling theorem of multi-dimensional signal to IBR. Basically, in high-dimensional space, rectangular sampling is not optimal any more and the generalized sampling method should be used. The sampling lattice should be hexagonal or quincunx. Such sampling lattice and the corresponding Fourier transform is shown below:
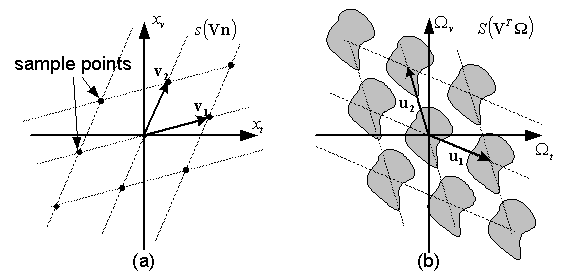
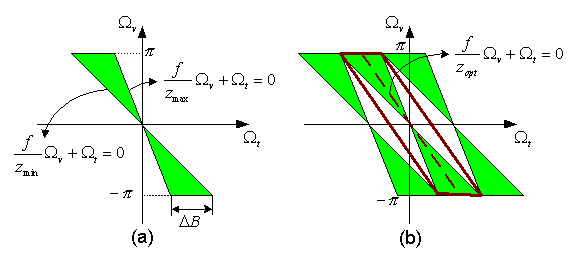
We use the first order spectrum approximation by Chai et al. in their 2000 SIGGRAPH paper. Basically, their conclusion is, the Fourier spectrum of IBR is bounded by the maximum and minimum distance of the scene, as well as the resolution of the capturing camera and rendering camera. A sketch of a scene's Fourier spectrum is shown below (figure (a)). They proposed to use the following way to pack the spectrum (figure (b)):
We proposed to pack it more compactly, as below:
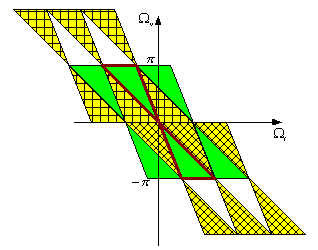
Obviously, we get a 100% usage of the frequency space.
Unfortunately, due to many reasons such as the error around DC frequency of the first order spectrum approximation, as well as occlusions and non-Lambertian effects, the above approach didn't work as well as we expected. Please refer to our technical report for more details.
| Publications |
- C. Zhang and T. Chen, "Surface Plenoptic Function: Spectral Analysis for Image-Based Rendering", submitted to CVPR2003, Madison, Wisconsin, USA, June, 2003.
- C. Zhang and T. Chen, "Surface Plenoptic Function: A Tool For the Sampling Analysis of Image-Based Rendering", submitted to ICASSP2003, Hong Kong, China, April 2003.
- C. Zhang and T. Chen, "On Generalized Sampling on Image-Based Rendering Data", ICASSP2003, Hong Kong, China, April 2003.
- C. Zhang and T. Chen, "Spectral Analysis for Image-Based Rendering Data", revised and re-submitted to IEEE Trans. on CSVT Special Issue on Image-based Modeling, Rendering and Animation.
- C. Zhang and T. Chen, "Towards Optimal Least Square Filters Using The Eigenfilter Approach", ICASSP 2002. , Orlando, FL, USA, May 2002.
- C. Zhang and T. Chen, "Spectral Analysis for Sampling Image-Based Rendering Data", Carnegie Mellon Technical Report: AMP03-01.
- C. Zhang and T. Chen, "Generalized Plenoptic Sampling", Carnegie Mellon Technical Report: AMP01-06.
Any suggestions or comments are welcome. Please send them to Cha Zhang.